Research Topics Max Herkerdorf
Excitation Signal Design for Nonlinear Dynamic Systems
The performance of data-driven techniques heavily depends on the quality of the data used for model training and validation. In the application of nonlinear system identification, these data sets are often not readily available and need to be generated using suitable excitation signals.
The approaches investigated are based on the principle that the information acquired by an excitation signal about a process is inherently linked to the distribution it generates within a model’s input space. Therefore, the excitation signal design methods presented here aim to optimize this distribution, facilitating the acquisition of accurate and comprehensive information about the process behaviors intended to be modeled.
OMNIPUS / IDS-FID Signal Generator
The OptiMized Nonlinear InPUt Signal (OMNIPUS) generator is designed to distribute data points across the model input space in a manner that ensures comprehensive coverage, reducing gaps and clustering [1]. This space-filling design is particularly suitable for the identification of nonlinear dynamic systems, as it enables data collection across the entire operational area, thereby capturing the full extent of nonlinear behavior. The method relies on an iterative procedure that concatenates optimal sequences, where "optimal" refers to the maximization of a sequence-based space-filling criterion. The criterion is computed using a rough model of the system, which requires minimal process knowledge. Such a proxy model is essential since, in practice, prior knowledge of the system is often limited, making direct access to the process input space infeasible.Building upon the OMNIPUS approach, the Incremental Dynamic Space-Filling Design (IDS-FID) signal generator represents an advancement with an adjusted optimization criterion. While it continues to prioritize the space-filling criterion, IDS-FID additionally allows for a user-defined focus on dynamic properties of interest during the data collection process [2]. Employing the example of a nonlinear first-order Hammerstein process, Fig. 1 illustrates this progression, showing a shift from enhanced acquisition of information about static process behavior in (a) to capturing more transient behavior in (b).
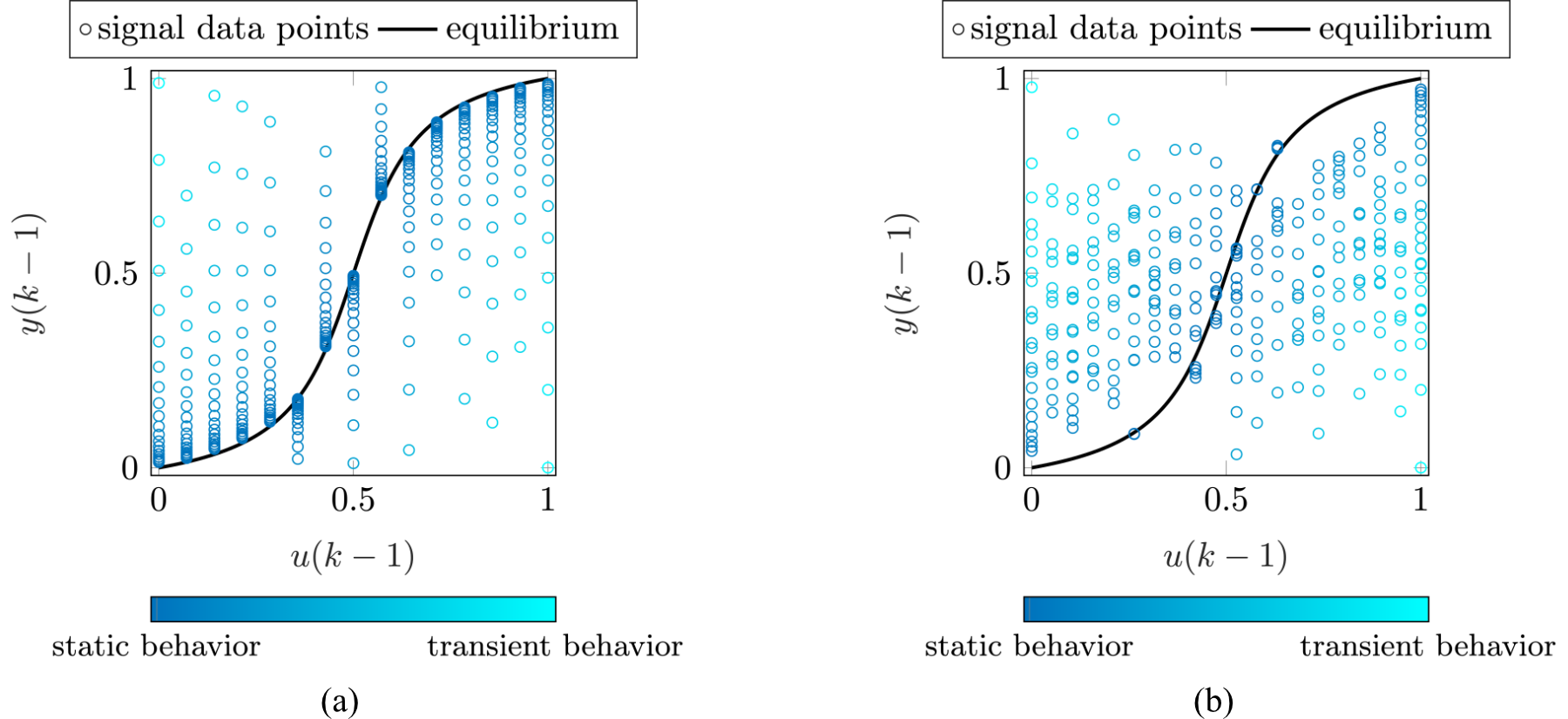 |
| Figure 1: Process input space distributions of a nonlinear first-order Hammerstein process generated from signals using the IDS-FID algorithm, prioritizing static responses in (a) and transient responses in (b). The space-filling criterion is concurrently addressed, as evidenced by the comprehensive coverage of the entire space. |
Receding Horizon Control-Inspired Signal Generator
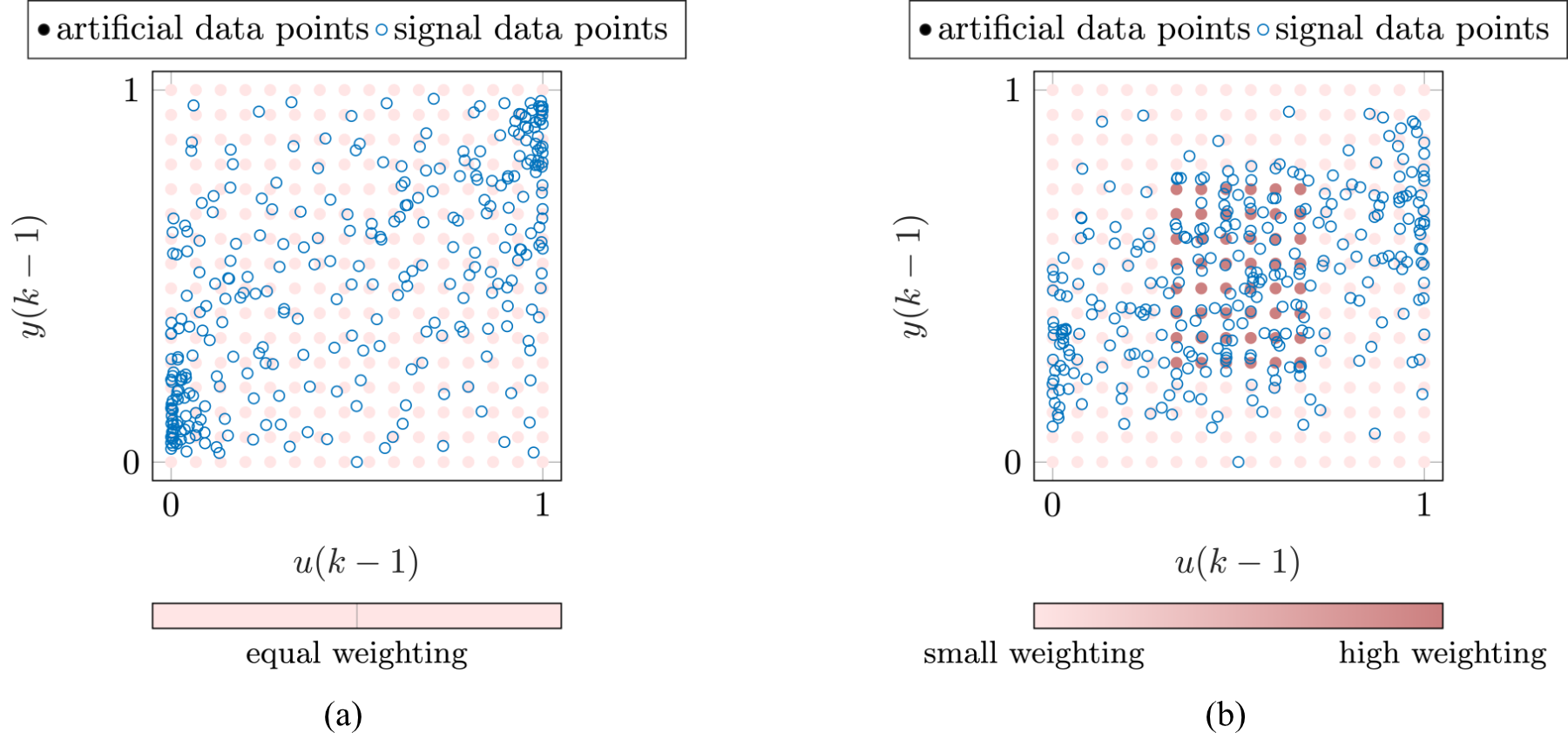 |
| Figure 2: Input space distributions of a nonlinear first-order Hammerstein process generated from signals using the RHC-inspired approach. In panel (a), an equal weighting scheme is applied, resulting in a high-quality space-filling design. Panel (b) demonstrates that, by employing an adjusted weighting scheme, certain regions can be given greater focus, facilitating targeted information acquisition. |
All the presented excitation signal design approaches are characterized by straightforward practical implemen-
tation, allowing them to meet industrial requirements effectively [4].
One-Class Classifier for Data Assessment
In the context of rapidly growing data volumes, not only is the design of excitation signals critical, but the evaluation of existing data sets also plays a significant role. Proper assessment allows for meaningful comparisons between data sets and aids in selecting appropriate training and validation data.
In the approach under investigation, again the positioning of data within the input space of a model is employed, with an envelope constructed around the data distribution using a one-class classifier (OCC). As shown in Fig. 3, the filling grade (fg), defined as the ratio of the enveloped area to the total input area, is employed as a metric for evaluating data quality with regard to the space-filling property.
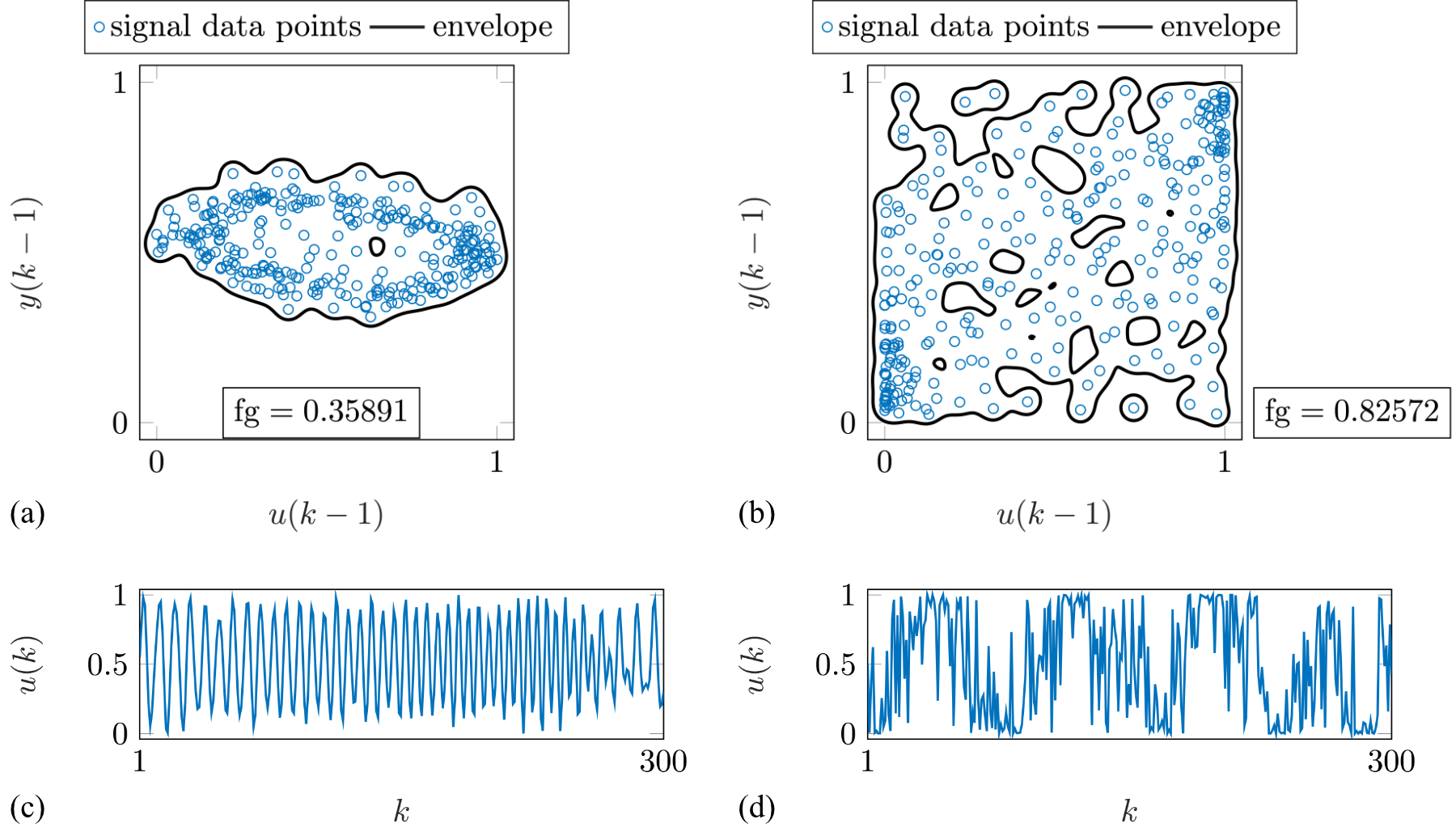 |
| Figure 3: Illustration of the OCC-envelope used as a space-filling criterion. The filling grade (fg) is calculated as the ratio of the area enclosed by the OCC-envelope to the entire input space, where a higher filling grade indicates more effective space coverage. |
A further potential application of the OCC-envelope lies in assessing the similarity between existing data sets. In this context, the overlapping regions of different envelopes represent the proportion of shared information between the data sets. Consequently, overlapping areas can be identified as similar, while non-overlapping regions signify novel information. This enables the selective inclusion or exclusion of data for training or validation, optimizing the data set by preventing gaps or unnecessary clustering.
References
| [1] | Tim Oliver Heinz and Oliver Nelles. “Iterative excitation signal design for nonlinear dynamic black-box models”. In: Procedia computer science 112 (2017), pp. 1054–1061 |
| [2] | Max Herkersdorf, Tarek Kösters, and Oliver Nelles. “Optimized Excitation Signal Tailored to Pertinent Dynamic Process Characteristics”. In: arXiv preprint arXiv:arXiv:2410.00500 (2024). |
| [3] | Max Herkersdorf and Oliver Nelles. “Optimized Excitation Signal Design Employing Receding Horizon Control”. In: arXiv preprint arXiv:arXiv:2410.00504 (2024). |
| [4] | Tarek Kösters, Tim Oliver Heinz, and Oliver Nelles. “Optimization based excitation signal design tailored to application specific requirements”. In: IFAC-PapersOnLine 55.37 (2022), pp. 451–456. |
Back to Overview
