Research Topics Timm Peter
Preprocessing for Data-Driven Modeling with Probability Density Estimation
Density-Based Subset Selection
In the context of data-driven modeling, the selection of a representative subset from a larger dataset is a challenging task, particularly when dealing with large amounts of data. Traditional methods like random sampling often fail to capture the underlying distribution of the data, leading to subsets that may not be representative. To address this challenge, a novel subset selection algorithm based on kernel density estimation (KDE) is developed in [3].
The algorithm aims to ensure that the selected subset represents either (1) the original dataset’s distribution or (2) an arbitrary distribution, for example the uniform distribution, as close as possible, see Fig. 1. It operates in a greedy or forward selection manner, meaning that one data point from the original dataset is selected after the other and added to the selected subset without replacement. The basis for the selection is the comparison of estimated kernel densities. For this purpose, the pdf of the original dataset is compared with the pdfs of candidate datasets. The candidate datasets consist of the selected data points and one non-selected data point each.
A key feature of this method is its computational efficiency. The algorithm evaluates the estimated density in a sophisticated manner that significantly reduces the computational load. The effectiveness of the density-based subset selection is demonstrated through various benchmark datasets and real-world applications, showing that it performs on par with or better than state-of-the-art methods in capturing the essential characteristics of a dataset.
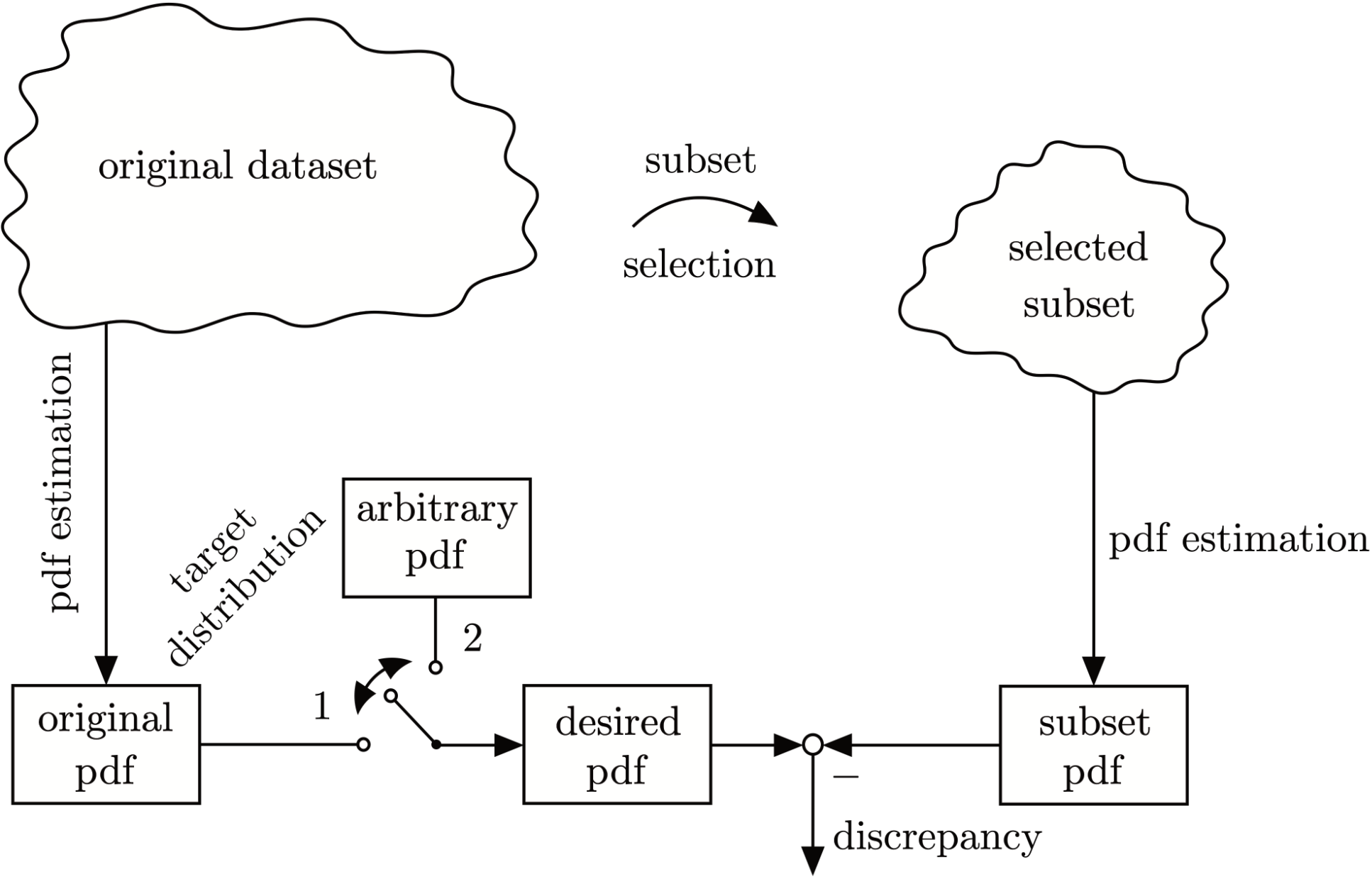
|
| Figure 1: Two cases to choose a desired pdf for subset selection with alternative goals. Either a subset is selected to (1) fit the original dataset's data distribution or (2) approximate an arbitrary target distribution. The minus sign, from which the discrepancy results, is to be understood symbolically and expresses the comparison of two distributions. |
Density-Based Data Weighting
Handling imbalances in dynamic datasets is a significant challenge in data-driven modeling. Datasets collected from real-world processes often exhibit imbalances, where certain operational regimes are overrepresented while others are underrepresented. This happens for example if regular operation takes place at only a few operating points. To mitigate this issue, a data weighting method is introduced in [2, 1], which adjusts the influence of individual data points using kernel density estimation.
The method extends the loss function by incorporating a weighting term that is determined by the inverse estimated data point density in the regressor space, see Fig. 2. In this way, data points in sparsely populated regimes of the regressor space are assigned higher weights, ensuring that they have a greater influence on the model training process. Conversely, data points from overrepresented regions receive lower weights.
This approach is validated through extensive testing with (nonlinear) autoregressive with exogenous input ((N)ARX) models on both linear and nonlinear dynamic datasets as well as real-world applications. The results consistently demonstrate improved model performance, especially for imbalanced datasets.
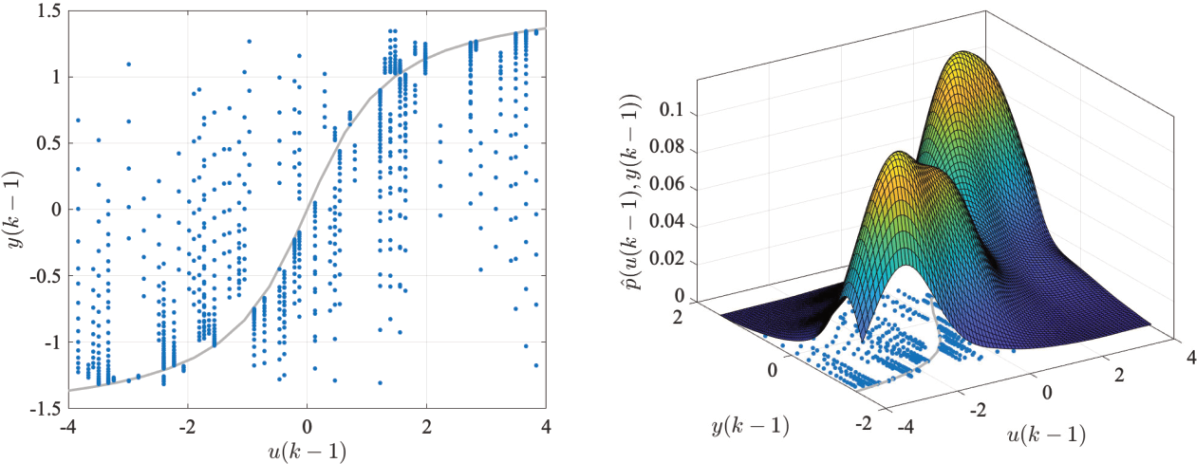
|
| Figure 2: Visualization of the density-based data weighting strategy. |
References
| [1] |
Timm J Peter, Tarek Kösters, and Oliver Nelles. “Density Estimation in the Regressor Space for Nonlinear System Identification”. In: IFAC-PapersOnLine 56.2 (2023), pp. 5849–5854. |
| [2] |
Timm J Peter and Oliver Nelles. “Density Estimation in the Regressor Space for Linear and Nonlinear System Identification”. In: IFAC-PapersOnLine 55.12 (2022), pp. 7–12. |
| [3] |
Timm J Peter and Oliver Nelles. “Fast and simple dataset selection for machine learning”. In: at-Automatisierungstechnik 67.10 (2019), pp. 833–842. |
Back to Overview
