Research Topics Hermann Klein
Nonlinear State Space System Identification
Nonlinear state space representations (NLSS) are the most general and abstract mathematical descriptions of dynamic systems. In comparison to common feedback approaches like Nonlinear Autoregressive models with eXogenous Inputs (NARX), nonlinear state space models
- are more powerful due to internal state feedback instead of output feedback,
- construct modeled state variables,
- require more sophisticated optimization techniques with recurrent gradients,
- can be easily expanded to multiple-input multiple-output (MIMO) processes.
The integration of neural networks into a state space framework generates a flexible black-box modeling approach for the identification of nonlinear processes. In particular, the Local Model State Space Network (LMSSN) has proven to be a powerful tool for accurately modeling various real-world applications as well as benchmark systems. (Figure 1 shows the block diagram of the LMSSN. For detailed information, see also [1].)
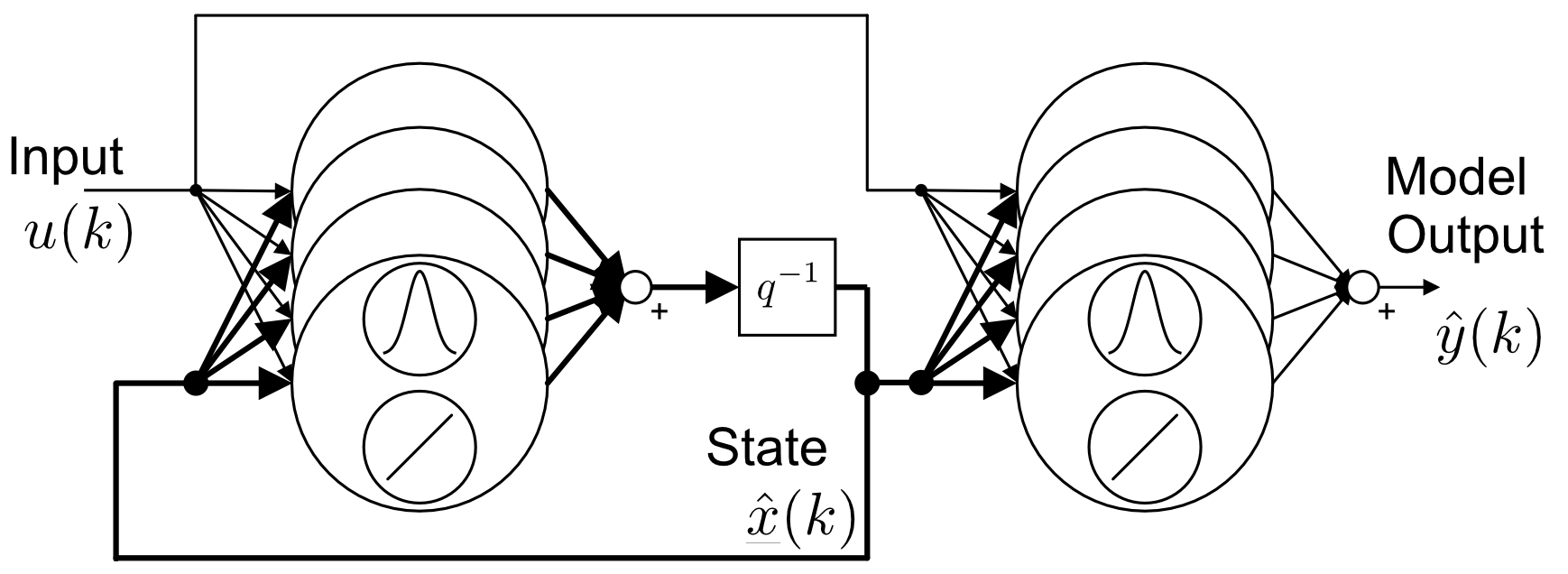 |
| Figure 1: Block diagram of the discrete-time Local Model State Space Network. |
In Machine Learning, recurrent neural networks (RNNs) like the Long Short-Term Memory (LSTM) or the Gated Recurrent Unit (GRU) are popular approaches for time series modeling. From a system identification perspective, RNNs can be seen as NLSS models. In contrast to RNNs NLSS models benefit under several aspects:
- Separation between the dynamic order and the number of neurons
- Lower number model parameters
- Comprehensibility of model parameters
- Compact representation
- Deterministic modeling leads to reproducibility
- Fewer tuning parameters
From a control-oriented perspective, LMSSNs are related to Takagi-Sugeno state space systems or linear-parameter varying (LPV) systems. Due to its local linear models, it aims at the middle-ground between linear and nonlinear modeling approaches.
In LMSSNs, the required global nonlinear approximators are generated through linear models which are active in local regions. A special feature of this approach is that these regions are learned from data in an efficient and demand-oriented manner, aided by tree-construction algorithms like the Local Linear Model Tree (LOLIMOT) or the Hierarchical Local Model Tree (HILOMOT).
Gray-Box State Space Modeling
Commonly, black-box modeling approaches yield a high modeling performance but are difficult, or even impossible, to interpret. If a successful identification task requires additional criteria beyond modeling performance, such as interpretability, sparsity, and robustness, gray-box modeling techniques offer advantages over black-box approaches. In addition to measurement data for parameter estimation, prior knowledge of the process is incorporated into model training. The purpose of this research is the development of general-purpose gray-box state space methods without restrictions to specific processes.
In engineering applications, prior knowledge is often available in form of a symbolic linear system of differential equations based on first principles. Gray-box state space identification incorporates prior knowledge by initializing with a linear model of the process. This linear model can contain various forms of prior knowledge, e.g.,
- physical parameters,
- interpretable state realization where state variable corresponds to physical quantities and/or
- relation between different state variables through a specific canonical form.
In the next step, this linear model is refined to match the true nonlinear process behavior. The Local Linear Model Tree algorithm can be used to learn the model’s operating- and state-dependent behavior while maintaining the initial interpretable structure.
With the help of this gray-box strategy, it is feasible to extract physical information from measured data, as the nonlinear effects are isolated within the model structure.
For example, unknown internal nonlinear dynamics can be captured by this proposed gray-box approach. Figure 2 below demonstrates the separation between a linear equation of motion and a hysteretic memory, suitable for modeling the Bouc-Wen benchmark dataset [2].
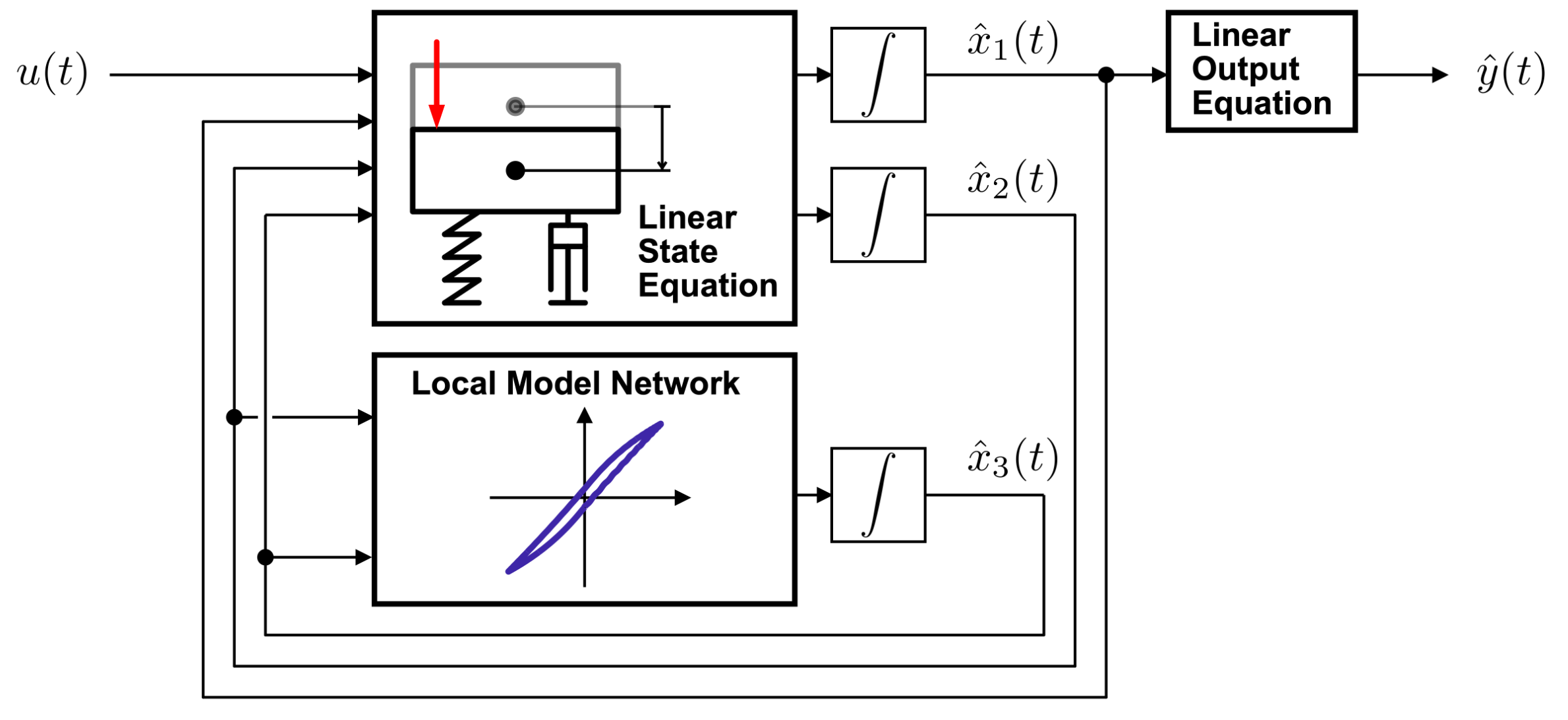 |
| Figure 2: Example for a Gray-Box LMSSN model for a hysteretic oscillator. |
References
| [1] | Max Schüssler. "Machine learning with nonlinear state space models". PhD thesis. Universität Siegen, 2022. |
| [2] | Hermann Klein and Oliver Nelles. "Identification of Gray-Box Hysteresis State Space Models". In: Book of Abstracts - 8. Workshop on Nonlinear System Identification Benchmarks: Lugano (Switzerland), 24.-26. April 2024. |
| [3] | Hermann Klein, Max Schüssler, and Oliver Nelles. "Physical Interpretabilty of Data-driven State Space Models". In: Proceedings - Workshop Computational Intelligence: Berlin, 23.-24. November 2023. |
| [4] |
Hermann Klein, Max Schüssler, and Oliver Nelles. "Physical-Inspired State Space Structure for Nonlinear Gray-Box Modeling". In: 10th International Conference on Control, Decision and Information Technologies (CoDIT). IEEE. |
Back to Overview
