Kurzanleitung für Scilab

Inhalt

Bedienung
Grundrechenarten
Vordefinierte Konstanten
Wichtige mathematische Funktionen
Matrixoperationen
Eine Funktion zeichnen
Polynome
Regelungstechnik
Eigene Funktionen definieren
Programmieren
Datenverwaltung
Nachtrag Regelungstechnik: Zustandsraummethoden

Bedienung (Inhalt)

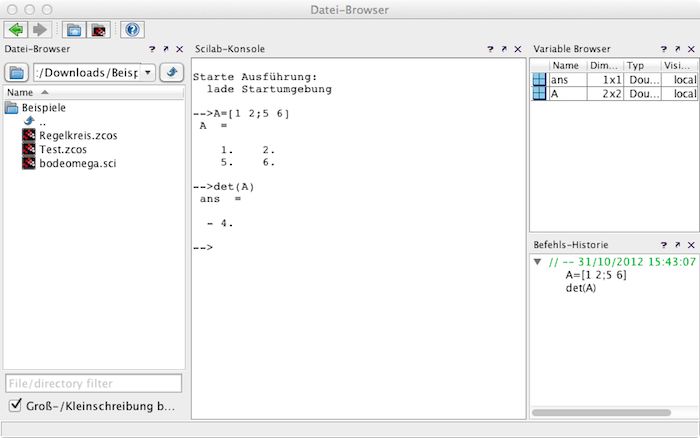
Nach dem Starten von Scilab erscheint das Kommandofenster (siehe Bild). Hinter dem pfeilförmigen Prompt --> können Sie nun Scilab-Befehle eingeben. Mit den Cursor-Tasten hoch/runter können Sie übrigens durch bereits früher eingegebene Befehle blättern. Mit den Cursor-Tasten links/rechts können Sie durch die eingegebene Befehlszeile laufen und den eingegebenen Text ändern (zum Löschen von Zeichen können Sie sowohl die DEL als auch die BACKSPACE-Taste in gewohnter Weise verwenden). Die Eingabe lässt sich mit der ESC-Taste abbrechen. Ein eingegebener Befehl wird nach Betätigen der Taste ENTER ausgeführt. Um einen Befehl in einer neuen Zeile fortzusetzen, beenden Sie die aktuelle Zeile mit ... (drei Punkte) und drücken Sie ENTER. Geben Sie den Rest des Befehls in die neue Zeile ein und drücken Sie ENTER um den Befehl auszuführen.
Hilfe im Programm erhalten Sie unter dem Menü-Eintrag Help->Help Dialog. Kennen Sie einen Befehlsnamen und wollen nähere Informationen, können sie auch help gefolgt von dem Ihnen bekannten Befehlsnamen, eintippen. Unter dem Menüpunkt Demos können Sie sich einige Beispiele ansehen.

Grundrechenarten (Inhalt)

+, -, *, ^ sind die Befehle für Addition, Subtraktion, Produkt und Potenz.

Auswertereihenfolge: 1+2*3-3^4*(2+5), diesen Term z.B. berechnet Scilab in der mathmatisch korrekten Reihenfolge von links nach rechts unter Berücksichtigung der Prioritäten von Potenzen (^), Produkten (*), Klammerausdrücken etc. und meldet: ans= -560
Standardausgabevariable: ans, ist die Standardvariable in der Scilab alle Ergebnisse speichert, wenn Sie keine Variable vorgeben.
Variable zuweisen: Wenn Sie das Ergebnis z.B. in der Variable Ergebnis speichern wollen, können Sie diese explizit durch Verwendung eines Gleichheitszeichens (=) vorgeben:
Ergebnis=1+2*3-3^4*(2+5)
Scilab meldet dann:
Ergebnis = -560.
Sie können nun bei weiteren Berechnungen die Variable Ergebnis weiterverwenden (z.B. 2*Ergebnis-50).
Ausgabe unterdrücken: Wenn Sie nicht wollen, dass Ihnen Scilab etwas zurückmeldet, so schließen Sie den Befehl mit einem Semikolon ab:
Ergebnis = 1+2*3-3^4*(2+5);
Scilab wird dann das Ergebnis der Variablen Ergebnis zuweisen, ohne es ihnen mitzuteilen.

Vordefinierte Konstanten (Inhalt)

Scilab stellt Ihnen eine Reihe von vordefinierte Konstanten zur Verfügung. Alle vordefinierten Konstanten beginnen mit einem Prozentzeichen.

%e, natürliche Zahl e=2.7182818...
%pi, Kreiszahl Pi=3.1415927...
%i, Imaginärzahl i^2=-1
%inf, Unendlich (Infinity)
%nan, keine Zahl (not a number), z.B. 1/0
%T, Wahr (True), Wahrheitwert in der Boolschen Logik
%F, Falsch (False), Wahrheitwert in der Boolschen Logik

Wichtige mathematische Funktionen (Inhalt)

Das Argument der Funktion wird stets innerhalb einer Klammer, die sich unmittelbar an den Funktionsnamen anschließt, an die Funktion übergeben. Das in den folgenden Beispielen verwendete Argument "x" steht für beliebige Zahlenwerte, von Ihnen zuvor definierte Variablen, bzw. jede Art von Ausdruck oder Scilab-Befehl der zu einem Zahlenwert ausgewertet werden kann. Sie können z.B. auch eine Funktion als Argument einer Funktion übergeben.

sqrt(x), berechnet die Quadratwurzel von x. Alternativ: x^0.5
exp(x), berechnet die x. Potenz der natürlichen Zahl e. Alternativ: %e^x
sin(x), asin(x), sinh(x) berechnet den Sinus von x (Bogenmaß), bzw. die Inversion des Sinus, bzw. den Sinushyperbolicus
cos(x), acos(x), cosh(x), Cosinus, inverser Cosinus, Cosinushyperbolicus
tan(x), atan(x), tanh(x), Tangens (Alternativ: sin(x)/cos(x)), inverser Tangens, Tangenshyperbolicus.
log(x), log10(x) natürlicher Logarithmus (Basis e), Logarithmus zur Basis 10

Matrixoperationen (Inhalt)

Definition einer Matrix: A=[1 2 3;4 5 6;10 11 12], definiert eine Matrix mit 3 Zeilen und 3 Spalten, die mit den angegebenen Werten gefüllt ist. Matrizen werden innerhalb eckiger Klammern definiert. Werte einer Zeile werden mit Leerzeichen oder Kommata voneinander getrennt. Eine neue Zeile beginnt man mit einem Semikolon. Scilab meldet in diesem Beispiel:
```
 A  =

   1.     2.     3.  
   4.     5.     6.  
   10.    11.    12.   
```
inv(A), berechnet die Inverse der Matrix A (A muss quadratisch sein).
A+B, (elementweise) Addition von zwei Matrizen (Matrizen A und B müssen die gleiche Dimension haben), oder Addition eines Skalars mit einer Matrix, z.B. 5+A (5 wird zu jedem Element der Matrix addiert).
A-B, siehe oben, allerdings Subtraktion.
A', Transponierte der Matrix A (Zeilen der Matrix werden zu Spalten und umgekehrt). Ist A ein Zeilenvektor wird er zum Spaltenvektor und umgekehrt.
A*B, Matrizenprodukt (Spaltenzahl der Matrix A muss gleich der Zeilenzahl der Matrix B sein), oder Multiplikation eines Skalars mit einer Matrix, z.B. 5*A (jedes Element von A wird mit 5 multipliziert)
A.*B, elementweise Multiplikation zweier Matrizen (müssen gleiche Dimension haben).
A/B , ist die Abkürzung für A*inv(B), da es keine Matrizendivision gibt. Ist A oder B ein Skalar, so wird jedes Element der Matrix durch den Skalar dividiert.
A./B, elementweise Division zweier Matrizen (müssen gleiche Dimension haben).
A^n, Abkürzung für mehrfache Matrizenmultiplikation von A mit sich selbst (A muss quadratisch sein). Zum Beispiel ist A^3 identisch mit dem Befehl A*A*A.
A.^n, elementweises Potenzieren einer Matrix (A kann beliebige Zeilen und Spaltenzahl haben). Zum Beispiel ergibt [1 2 3].^2 den Vektor [1 4 9]
det(A), berechnet die Determinante von A.
Colon-operator: Sie können den Doppelpunkt (Colon) benutzen, um größere Vektoren aufzubauen. Der Befehl x=[0:0.1:100] erzeugt Beispielsweise einen Zeilenvektor, der die Zahlenwerte 0, 0.1, 0.2 ... 100 enthält. Wie Sie sehen, werden - durch Doppelpunkt getrennt - Startwert, Schrittweite und Endwert angegeben. Lassen Sie die Schrittweite weg, so nimmt Scilab eine Schrittweite von 1 an. Beispiel: x=[0:5] ergibt den Vektor x=[0 1 2 3 4 5]
zeros(x,y) erzeugt eine mit Nullen gefüllte Matrix mit x Zeilen und y Spalten.
ones(x,y), erzeugt eine mit Einsen gefüllte Matrix mit x Zeilen und y Spalten
eye(x,y), erzeugt eine Matrix mit x Zeilen und y Spalten, deren Hauptdiagonalelemente 1 und deren restl. Elemente 0 sind. Ist x=y so ergibt sich die eine quadratische Einheitsmatrix I.
Einzelne Werte eines Vektors x erhalten Sie mit dem Befehl x(i), wobei i=1 der erste Wert im Vektor ist. Den Index des letzten Wertes erhalten Sie mit dem Befehl size(x). Sie können sich auch Bereiche des Vektors ausgeben lassen, indem Sie den Colon-Operator (:) verwenden. Mit x(5:10) erhalten Sie z.B. einen Vektor, der die Werte des Vektors x an den Positionen 5 bis 10, enthält.
Einzelne Werte einer Matrix A erhalten Sie mit A(i,j), wobei i die Zeilen- und j die Spaltennummer des Elements angibt. Auch hier können Sie sich Bereiche (Untermatrizen) ausgeben lassen. A(1:3,6:9) liefert z.B. eine Matrix, die die Elemente der ersten 3 Zeilen und der Spalten 6 bis 9 von A enthält. Möchten Sie eine komplette, z.B. die zweite, Spalte von A extrahieren, können Sie folgende Schreibweise verwenden: A(:,2). Die Größe der Matrix A erfragen Sie mit mit size(A). Sie erhalten einen Vektor, dessen erstes Element die Zeilenzahl und des zweites Element die Spaltenzahl von A enthält.

Eine Funktion zeichnen (Inhalt)

plot2d(x,F), öffnet ein Grafikfenster und zeichnet die Werte aus dem Vektor F über den Werten aus Vektor x. Um zu Beispiel eine quadratische Parabel für Zahlenwerte von 0 bis 100 zu zeichnen geben Sie ein:
x=[0:0.01:100]; F=x.^2; plot2d(x,F)
Der Plotbefehl hat viele Parameter, z.B. zur Bestimmung von Linienart, Farbe, Achsenskalierung usw., zudem gibt es die Variante plot3d für 3D-Plots. Für weitere Details empfiehlt es sich, mit help plot2d die Online-Hilfe dieses Befehls aufzurufen.
clf, löscht den letzten Plot (clear last figure). Führen Sie den plot-Befehl ohne vorheriges Löschen erneut aus, so wird die neue Kurve zum bestehenden Plot hinzugezeichnet.
xgrid(), schaltet Gitterlinien im Plot an.
replot([xmin,ymin,xmax,ymax]), zeichnet einen Plot neu und setzt die Achsen auf die von Ihnen gewünschten Maximal- und Minimalwerte xmin,ymin,xmax,ymax.
square(), macht das Grafikfenster quadratisch.

Polynome (Inhalt)

Sie können bei Scilab mit Polynomen arbeiten. Polynome müssen zunächst mit dem Befehl poly definiert werden, danach kann man sehr bequem, z.B. für regelungstechnische Berechnungen, Übertragungsfunktionen definieren. Polynome können sogar in Matrizen verwendet werden, was für Zustandsraum-Methoden sehr nützlich ist.

P1=poly([1 2 3 4],'s'), dieser Befehl erzeugt ein Polynom mit den Nullstellen 1, 2, 3 und 4 und legt den Buchstaben s als Variable des Polynoms fest. Man erhält das Polynom: 24-50s+25s²-10s³+s⁴.
P2=poly([1 2 3 4],'s','coeff'), erzeugt ein Polynom mit den Koeffizienten 1, 2, 3 und 4. Man erhält: 1+2s+3s²+4s³
s=poly(0,'s'), legt die Variable s als Polynomvariable fest. Wenn diese Festlegung einmal erfolgt ist, können Sie das Polynom (auch Brüche) einfach eintippen, z.B.: P3=(s+1)/(s^2+3*s+4)
roots(P), berechnet die Nullstellen des Polynoms P.
P1*P2, P1/P2, P1+P2, P1-P2, Polynome lassen sich natürlich multiplizieren, dividieren, addieren und subrahieren. So ergibt z.B. P1*P2 mit den obigen Beispielwerten für P1 und P2: 24-2s+7s²+6s³-114s⁴+112s⁵-37s⁶+4s⁷
horner(P,x), berechnet den Zahlenwert des Polynoms P für einen Zahlenwert x, der anstelle der Polynomvariable (in den vorherigen Beispielen 's') eingesetzt wird (x kann auch ein Vektor sein, dann liefert horner einen Vektor als Ergebnis). Z.B.: horner(P2,[1 2]) ergibt [10 49].

Regelungstechnik (Inhalt)

Scilab kennt einige Befehle zur Analyse von dynamischen Systemen. Dieser Abschnitt beschränkt sich auf Systeme mit einem Ein- und einem Ausgang (SISO). Für Systeme mit mehreren Ein- und Ausgängen empfiehlt sich die Zustandraumdarstellung, die auch von Scilab unterstützt wird. Näheres dazu im im Nachtrag Regelungstechnik: Zustandsraummethoden.

G=syslin('c',PZ,PN), oder G=syslin('c',PZN), definieren ein (kontinuierliches) lineares System mit dem Zählerpolynom PZ und dem Nennerpolynom PN, oder dem Bruch aus Polynomen PZN. Die Polynome müssen zuvor, wie im vorherigen Abschnitt erläutert, definiert werden. Ein P-T1 System mit T1=1 könnte also wie folgt definiert werden:
s=poly(0,'s'); P1=1; P2=s+1; G=syslin('c',P1,P2), oder:
s=poly(0,'s'); P=1/(s+1); G=syslin('c',P)
Das Polynom kann auch innerhalb des syslin-Befehls definiert werden: s=poly(0,'s');G=syslin('c',1/(s+1))
Die Definition s=poly(0,'s') muss übrigens nur einmal während einer Scilab-Sitzung erfolgen. Statt der Polynome können auch die Systemmatrizen angegeben werden, näheres erfahren Sie mit dem Befehl help syslin
nyquist(G,freqmin,freqmax), zeichnet für das zuvor mit syslin definierte System G die Frequenzgangortskurve für Frequenzen von freqmin bis freqmax.
evans(G,Kmax), zeichnet die Wurzelortskurve des zuvor mit syslin definierten Systems G für Reglerverstärkungen von 0 bis Kmax.
y=csim('step',t,G), berechnet die Sprungantwort des zuvor mit syslin definierten Systems G für die im Vektor t angegebenen Zeiten (z.B. mit t=[0:0.01:50] vorher definieren) und speichert sie in y ab. Das Ergebnis kann dann z.B. mit plot2d(t,y) dargestellt werden. Statt 'step' kann auch 'impulse' angegeben werden, um die Impulsantwort zu erhalten. Auch andere Funktionen oder Angabe von Stützpunkten eines beliebigen Eingangssignales ist möglich. Für ein sinusförmiges Eingangssignal können Sie y=csim(sin(t),t,G) eingeben.
bode(G,freqmin,freqmax), zeichnet das Bodediagramm des zuvor mit syslin definierten Systems G für einen Frequenzbereich von freqmin bis freqmax. Beachten Sie, dass der Befehl ein Bodediagramm erzeugt, dessen x-Achse die Frequenz in Hertz und nicht die Kreisfrequenz darstellt. Wenn Sie also Eckfrequenzen ablesen und in Parameter des Systems umrechnen wollen, müssen Sie die Frequenzen zuerst mit der Beziehung omega=2*Pi*f in die Kreisfrequenz umrechnen!!! Alternativ können Sie aber auch folgenden Weg gehen:
1. [frq,repf]=repfreq(G,freqmin,freqmax), berechnet den Frequenzgang des Systems G für den Frequenzbereich von freqmin bis freqmax. Die Funktion liefert als Ergebnis den Vektor repf der den Frequenzgang in Form von komplexen Zahlen enthält und den Vektor frq mit den zugehörigen Frequenzen.
2. [phi,amp]=phasemag(repf), mit diesem Befehl erhalten Sie nun aus dem Vektor repf einen Vektor amp der die Amplitude in db und einen Vektor phi der die Phaseverschiebung in Grad enthält.
3. plot2d('ln',frq*2*%pi,amp), zeichnet den Amplitudengang nun in der gewohnten Form über der Kreisfrequenz (die Frequenzwerte frq werden in der Darstellung einfach mit 2*Pi multipliziert). Der Parameter 'ln' zeigt an, dass die x-Achse logarithmisch ('l') und die y-Achse normal ('n') skaliert werden soll.
4. plot2d('ln',frq*2*%pi,phi), zeichnet den Phasengang in der gewohnten Form über der Kreisfrequenz.
  Vergessen Sie nicht den Amplitudengang mit clf zu löschen, bevor Sie den Phasengang zeichnen. Gitternetzlinien erhalten Sie mir dem Befehl xgrid()
xcos(), startet den Blockschaltbildeditor und ermöglicht die graphische Eingabe (Blockschaltbild) und Simulation von dynamischen Systemen (kontinuierlich und diskret).

Eigene Funktion definieren (Inhalt)

Wem z.B. die oben geschilderte Vorgehensweise zur Darstellung des Bodediagramms zu aufwändig ist, der hat die Möglichkeit eine Funktion zu schreiben, die diese Aufgabe übernimmt. Eigene Funktionen müssen bei der Definition mit dem Befehl function begonnen und mit dem Befehl endfunktion beendet werden. Direkt hinter dem Befehl function werden die Größen, die die Funktion zurückgibt, der Funktionsname und die Parameter, die der Funktion bei deren Aufruf übergeben werden, festgelegt. Das sieht z.B. so aus: [a,b,c]=meinefunktion(x,y). Die Funktion heißt meinefunktion, übernimmt die Parameter x und y und gibt nach Beendigung aller Berechnungen den Inhalt der Variablen a,b und c zurück.

Kurze Funktionen können direkt wie ein Befehl am Prompt im Kommandofenster eingegeben werden:
function y=summe(x1,x2), y=x1+x2, endfunction, durch Eingabe dieser Zeile erhält man eine (zugegebenermaßen nicht sehr sinnvolle) Funktion, die zwei Zahlen addiert. Sie können nun, um z.B. 2 und 3 zu addieren und in der Variable z zu speichern, den Befehl z=summe(2,3) eingeben.
Für umfangreichere Funktionen, empfiehlt es sich, diese im mitgelieferten Editor SciNotes (öffnen mit erstem Knopf oben links in der SciLab-Konsole) einzugeben und abzuspeichern (Textdatei mit Endung .sci). Solche Dateien können Sie mit Hilfe des Dateimenüs in die Arbeitsumgebung laden und stehen dann zur Ausführung bereit.
Um das Bodediagramm über der Winkelgeschwindigkeit bequem mit einem Befehl zu erhalten, geben Sie z.B. folgende Zeilen in SciNotes ein (diese Funktion ist in der Beispieldatei enthalten):

function bodeomega(G,freqmin,freqmax,plot_was)
[frq,repf]=repfreq(G,freqmin,freqmax);
[phi,amp]=phasemag(repf);
clf;
if plot_was=='p' then plot2d('ln',frq*2*%pi,phi)
else
plot2d('ln',frq*2*%pi,amp)
end
xgrid();
endfunction

Speichern Sie diese Datei unter dem Namen bodeomega.sci ab. Nachdem Sie diese Datei mit getf('Pfad\bodeomega.sci') importiert haben, können Sie sich mit dem Befehl bodeomega(G,fmin,fmax,'a') den Amplitudengang und mit bodeomega(G,fmin,fmax,'p') den Phasengang des Systems G im Frequenzbereich fmin bis fmax anzeigen lassen.

Programmieren (Inhalt)

Wie Sie vielleicht schon bei der obigen Funktion bodeomega bemerkt haben, können Sie mit dem if/else-Befehl Fallunterscheidungen durchführen. Scilab beherrscht aber auch noch andere Befehle zur Steuerung des Programmablaufes, z.B. die For-Schleife. Die Syntax dieser Befehle wird nun an Hand von Beispielen verdeutlicht:

if a>0 then y=1, elseif a<0 then y=-1, else y=0, end, ist eine Beispiel für eine Fallunterscheidung mit einer if/else-Struktur, sie entspricht der Signum-Funktion sign(a). Zunächst, unmittelbar hinter dem if-Schlüsselwort, wird ein Vergleich durchgeführt. Ist dieser Vergleich wahr, wird der Befehl hinter dem then-Schlüsselwort ausgeführt, dass heißt der Variable y wird der Wert 1 zugewiesen und die Bearbeitung der if/else-Struktur wird an dieser Stelle beendet. Ist der Vergleich falsch, so wird der Vergleich hinter dem elseif-Schlüsselwort überprüft, ist dieser wahr, so wird y der Wert -1 zugewiesen und die Struktur beendet. Hier können noch beliebig viele weitere Vergleiche mit Hilfe weiterer elseif-Schlüsselwörter eingefügt werden. Sollte die if-Bedingung und alle elseif-Bedingungen falsch sein, so wird der Befehl nach dem else-Schlüsselwort ausgeführt. Ist kein else vorhanden, würde in diesem Falle kein Befehl ausgeführt. Die Befehle müssen keine Zuweisungen sein wie in diesem Beispiel sondern es ist jede Art von Scilab-Befehl zulässig. Bitte nicht vergessen, jede if/else-Struktur muss mit einem end-Schlüsselwort beendet werden!
Folgende Vergleichsoperaturen sind weiterhin zulässig:
- Vergleich auf Gleichheit: a==b
- Größer oder gleich: a>=b
- Kleiner oder gleich: a<=b
- Ungleich: a~=b
Sowie die logischen Verknüpfungen:
- Logisches UND: &
- Logisches ODER: | (Senkrechter Strich, Pipe)
- Logisches NICHT: ~ (Tilde)
for i=1:2:5, x(i)=i^2, end, bei einer For-Schleife wird der Bereich zwischen den Schlüsselwörtern for und end mehrfach wiederholt und dabei eine Laufvariable bei jedem Durchlauf um einen bestimmten Wert erhöht, bis diese einen festgelegten Maximalwert erreicht hat. In diesem Beipiel durchläuft die Variable i die Werte 1, 3 und 5 und speichert dabei in einen Vektor x an die Positionen 1, 3 und 5 die Werte 1, 9 bzw. 25. Startwert, Schrittweite und Endwert der Laufvariable werden in der schon bekannten Weise, durch Doppelpunkt voneinander getrennt, angegeben. Auch hier muss ein end-Schlüsselwort die Struktur abschließen.

Datenverwaltung (Inhalt)

who, zeigt ihnen die Namen aller Variablen an, die zur Zeit definiert sind.
clear x, löscht die Variable mit dem Namen x aus dem Speicher.
save('test.dat',x), speichert den Inhalt der Variablen x in einer Binärdatei namens test.dat im aktuellen Verzeichnis auf der Festplatte ab.
save('dateiname.dat'), speichert den Inhalt aller Variablen, die zur Zeit definiert sind in einer Binärdatei namens dateiname.dat im aktuellen Verzeichnis auf der Festplatte ab.
load('test.dat'), lädt die in der Datei test.dat abgespeicherten Variablen wieder in die Arbeitsumgebung, dabei werden auch die Variablennamen wieder hergestellt.
chdir('Pfad'), Verzeichniswechsel, Pfad wird das neue aktuelle Verzeichnis.
chdir('..'), Verzeichniswechsel, das eine Stufe höher gelegene Verzeichnis wird aktuelles Verzeichnis
pwd, zeigt das aktuelle Verzeichnis an.

Nachtrag Regelungstechnik: Zustandsraumdarstellung (Inhalt)

Wie bereits im Abschnitt Regelungstechnik angedeutet, kann man bei Scilab auch mit den Methoden das Zustandsraumes arbeiten.

Geben Sie ein System in Zustandsschreibweise an: A=[1 2;-3 -4], B=[1 0;2 5], C=eye(2,2) (quadratische Einheitsmatrix I mit der Dimension 2), D=zeros(2,2) (quadratische Matrix mit Nullen, kein Durchgriff).
Die charakteristische Gleichung erhält man nun mit CGl=det(s*eye(2,2)-A) (ergibt: s²+3s+2). Zuvor müssen Sie allerdings die Variable s mit s=poly(0,'s') als Polynomvariable definiert haben. Mit roots(CGl) erhalten Sie nun ganz einfach die Pole des Sytems (in diesem Fall -1 und -2, das System ist also stabil).

Die Matrix der Übertragungsfunktionen (die die Ausgänge mit den Eingängen des Systems verknüpft) berechnen Sie mit G=C*inv(s*eye(2,2)-A)*B+D. Sie erhalten:

G  =

     8 + s            10        
   -----------   ------------   
             2              2   
   2 + 3s + s     2 + 3s + s  
                              
    - 5 + 2s       - 5 + 5s    
   -----------   ------------   
             2              2 
   2 + 3s + s     2 + 3s + s

Sie können nun auf jede einzelne dieser 4 Übertragungsfunktionen mit G(1,1) , G(1,2), G(2,1) und G(2,2) zugreifen und für weitere Untersuchungen verwenden. Z.B. können Sie die Sprungantwort von G(1,1) mit folgenden 3 Schritten ermitteln:
1. Übertragungsfunktion definieren: G11=syslin('c', G(1,1))
2. Zeitvektor definieren: t=[0:0.01:10]
3. Sprungantwort berechnen und darstellen: y=csim('step',t,G11);plot2d(t,y)
Dieses Beispiel liefert aber nur den Anteil der ersten Ausgangsgröße (y1), den die erste Eingangsgröße (u1) verursacht (bzw. es wird angenommen u2 wäre gleich Null). Wenn Sie z.B davon ausgehen, das beide Eingangsgrößen identische Sprünge sind, können Sie die vollständigen Ausgänge des Systems folgendermaßen berechnen:
- Ausgangsgröße 1: G11=syslin('c',G(1,1)); G12=syslin('c',G(1,2)); y1=csim('step',t,G11+G12).
- Ausgangsgröße 2: G21=syslin('c', G(2,1)); G22=syslin('c', G(2,2)); y2=csim('step',t,G21+G22).
Haben die Eingangsgrößen jedoch unterschiedliche Verläufe, dann empfiehlt es sich folgendermaßen vorzugehen:
1. Berechnen Sie direkt aus den Matrizen A,B,C und D die Übertragungsfunktion mit dem Befehl: GS=syslin('c',A,B,C,D)
2. Definieren Sie eine Funktion z.B. ut(t), die die Werte der Eingangsgrößen als Funktion des Zeitvektors t beschreibt und als Spaltenvektor zurückgibt. Ein Beispiel dafür wird anschließend gezeigt.
3. Simulieren Sie das System und stellen Sie es dar: y=csim(ut,t,GS);plot2d(t,y'). Beachten Sie, dass ut hier die Funktion ist, die im vorherigen Schritt definiert wurde. Für y ergibt sich durch csim für dieses Beispiel eine zweispaltige Matrix, da das System 2 Ausgänge hat. Zur Darstellung mittels plot2d muss die Transponierte y' verwendet werden, da t als Zeilenvektor definiert wurde. plot2d stellt die Verläufe von y1 und y2 verschiedenfarbig im gleichen Fenster dar.
Wie definiert man nun die Funktion ut. Nehmen wir an, zu Beginn soll nur die erste Eingangsgröße (u1) von 0 auf 1 springen, u2 springt erst zum Zeitpunkt t=10 auf 2, dann sieht die Funktionsdefinition wie folgt aus:
function u=ut(t), if t<10 then u=[1;0], else u=[1;2];end;endfunction
Wenn t kleiner 10 ist wird der Vektor [1;0], sonst der Vektor [1;2] zurückgegeben. csim erwartet die Werte der Eingangsgrößen in einem Spaltenvektor, dessen Zeilenzahl der Zahl der Eingangsgrößen entspricht. Sie sind bei der Definition von ut natürlich nicht auf Sprünge festgelegt, Sie können jede beliebige Funktion implementieren, z.B. eine Sinus- und eine Cosinusfunktion mit abklingender Amplitude:
function u=ut(t), u(1,1)=1/(t+1)*sin(t);u(2,1)=1/(t+1)*cos(t);endfunction

Viel Erfolg beim Experimentieren wünscht Ihnen das MRT-Team

Aktualisiert via XIMS am 30.4.2019 von G. Kampmann