Research Topics Tarek Kösters
Adaptive Local Model Networks (ALMN)
System identification is the task to estimate dynamic models from finite, noisy measurement data. Two identification scenarios can be distinguished. If data of the process have been collected and subsequently a model of the process is estimated, the procedure is called offline system identification. In contrast, when the data are presented as single data samples and the model is updated with respect to the given sample, the task is referred to as online identification. Typically, two reasons account for the deployment of online identification. One reason is the absence of a dataset to estimate a process model offline. A second more common reason is the application of the model in a time-variant scenario, which means that the process changes over time.
My work deals with the second case. My research focuses on the utilization of local model networks (LMNs) for this purpose. The mathematical framework of an LMN is based on the weighted superposition of different local linear models. This allows to employ least squares or the recursive least squares algorithm to estimate the local model parameters offline or online, respectively [7, 6]. Our work primary focuses on two aspects of the adaptation. On the one hand, we investigate different adaptation methods to realize a situation-dependent update behavior of the local model parameters. For this purpose, we especially focus on the incorporation of regularization and time-variable forgetting factors into the adaptation method [3, 2]. This allows for different model updates based on the current excitation situation as well as the present process variation.
On the other hand, we work on the effective utilization of local and global update strategies. In general, adaptation of the local model parameters results in local updates of the complete model, which means, that the model strictly only changes in regions where new data are present. This typically, enhances the robustness of the adaptation in comparison to globally defined model structures (e. g. polynomials) especially for unbalanced excitation scenarios. However, if global shifts in the whole process are present, global updates might be needed. For this purpose, we developed a global model extension and its corresponding adaptation algorithm, which can be seen in Fig. 1. With the global update of the model only simple changes of the model behavior can be made, which, however, influence the model globally. The local updates, in contrast, achieve complex model updates that influence the model only locally.
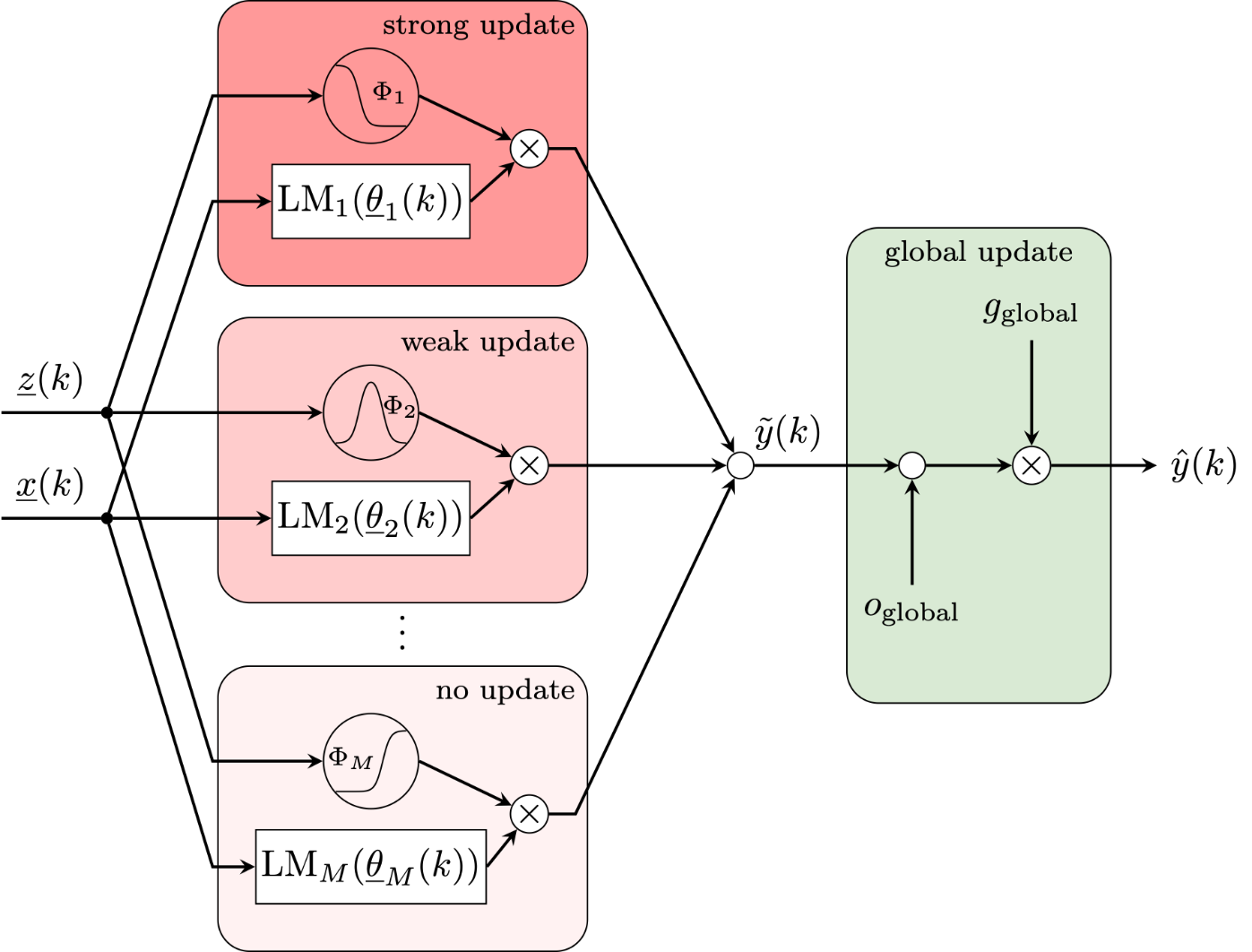 |
| Figure 1: Local model network with global and local adaptation possibilities. |
Process Optimization of a Combine Harvester
As application example our work centers around the combine harvester separation process. A combine harvester integrates the task to collect and separate grain crops into its components. Their main task is to exclude the valuable grains from the rest of the plant, which takes place in the threshing, separation and cleaning section of the combine harvester, see Fig. 2. In this process various adjustment options account for different situations the combine harvester encounters. Through the interaction of the combine harvester with natural materials and various crop types, optimal process settings are not known beforehand nor constant through the harvesting process.

|
| Figure 2: Typical distribution of combine harvester tasks along the machine body (adopted from [1]) |
The goal of this work is to optimally set the adjustment options the combine harvester offers, to manipulate the separation process, given the current operating conditions. For this purpose, a model-based optimization algorithm is utilized, see Fig. 3. To account for the variable conditions the combine harvester encounters, no time-invariant models are utilized, but a model adaptation is employed. It utilizes Adaptive Local Model Networks (ALMN) as explained above, to adapt the model with respect to the encountered conditions [5, 4]. This in turn allows the optimization to adjust the combine harvester settings correspondingly.
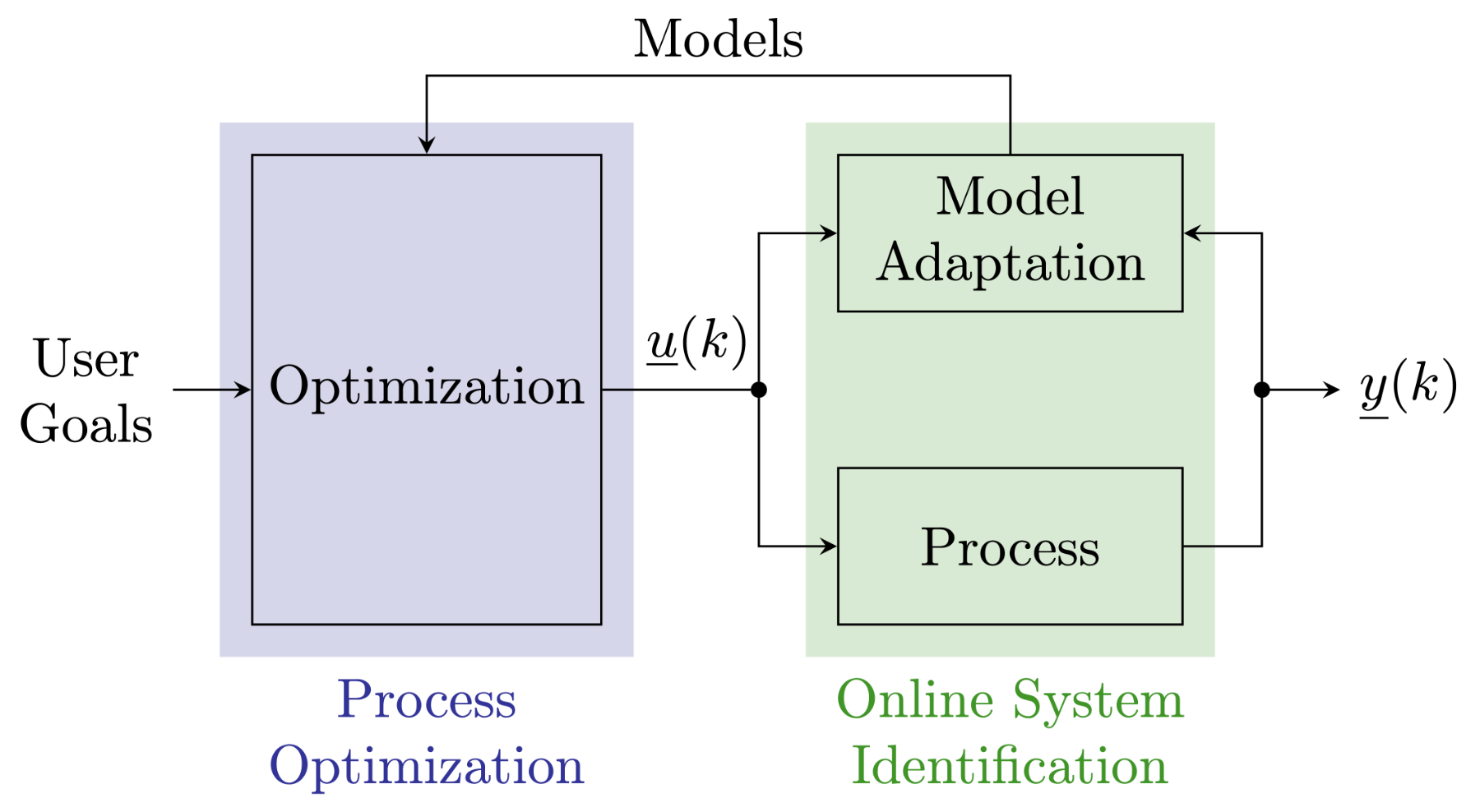
|
| Figure 3: Process optimization scheme for combine harvester separation process. |
References
| [1] | Deere & Company. X Series Combines. Online. 2023. |
| [2] | E. Horita et al. “A leaky RLS algorithm: its optimality and implementation”. In: IEEE Transactions on Signal Processing 52.10 (2004), pp. 2924–2936. |
| [3] | Christopher Illg et al. “Adaptive System Identification with Regularized FIR Models”. In: IFAC-PapersOnLine 55.12 (2022), pp. 1–6. |
| [4] |
Tarek Kösters and Oliver Nelles. “Adaptive Nonlinear Dynamic System Identification for Separation Process of Combine Harvester”. In: AgEng 2024 Athens. 2024, pp. 301–307. |
| [5] | Tarek Kösters and Oliver Nelles. “Nonlinear Dynamic System Identification of Separation Unit for Raw Materials”. In: 2023 IEEE Conference on Control Technology and Applications (CCTA). 2023, pp. 992–997. |
| [6] |
Edwin Lughofer. Evolving Fuzzy Systems - Methodologies, Advanced Concepts and Applications. Berlin, Heidelberg: Springer, 2011. |
| [7] |
Oliver Nelles. Nonlinear System Identification. Springer International Publishing, 2020. |
Back to Overview
